一、为什么现在还写高频因子?被限制了的写来有什么意义吗?
个人认为这类型因子反而不是在被限制范围内。可以去回顾之前的新闻,已有量化私募收到指令,达到高频交易认定标准的话流量费回提高10倍,从每笔委托0.1元提高到1元,每笔撤单费为5元的。而可能达到这个标准的策略比如:套利策略、做市商策略以及盘口策略。其中套利策略可以提高开仓的价差阈值来减少交易次数提高盈亏比的方法来避免被认定为高频。而盘口策略就影响大了,盘口策略大多数都是基于订单薄的数据进行计算的,典型的有Penny Jump策略,例如下图:
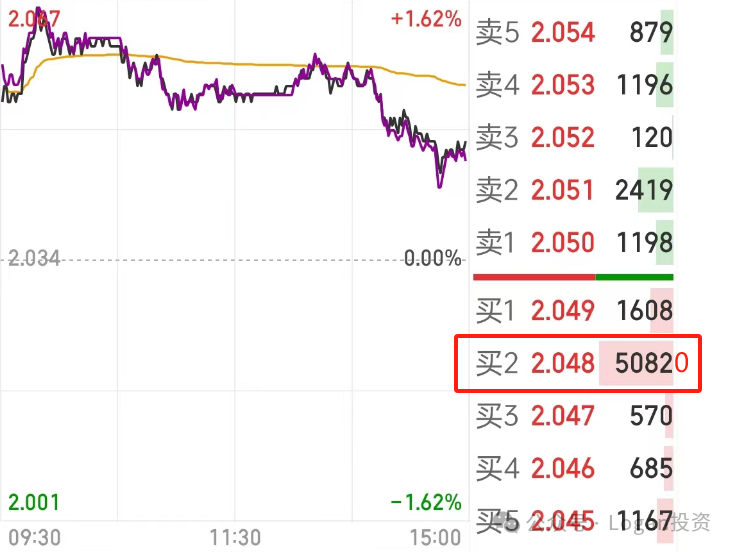
豆粕ETF7月26日的订单薄,买二(bid 2)有1608手买单,假设买三(bid 3)有50820手,这个时候就出现了Penny Jump认为的市场出现“大玩家”并支撑特定价格的情况,于是策略就会在这时的买一价挂单买入,买入之后立刻挂卖一或者卖二(ask 1 or ask 2)来卖出,总之就是卖在能覆盖交易成本同时能赚一点小钱的位置,就是凭概率硬赌它能卖出去,毕竟最后总有这个买二档的“冤大头大玩家”接盘,大不了最后卖给他然后亏一个tick的价格嘛~~,做的就是这个盈亏比。
但是使用Penny Jump策略的人发现,咦~ bid 2的委托买单逐渐减少到只剩下1000手了,那么谁还会傻乎乎的还在bid 1的价格挂单呢,这肯定会在策略上写一个if判断条件来撤单的嘛!
另一点,如果本身bid 2的委托买单就是假的呢?就是有人专门针对Penny Jump策略来做的虚假买单来骗你买进,并且到时候会大规模撤单的那种呢?
所以这时候这个委托单的数据就很不真实了,这也是监管局不想看到的情况之一。所以近期正式限制了以该类型策略为代表的高频交易,设置了撤单费,增加交易成本等措施。
话说回来,盘口策略不止这类型,也有基于订单薄委买委卖的成交量数据做的因子并产生的策略,这也是下文要讲的这个因子。那么在没限制以前,大规模的假单就使得基于委买卖量计算的因子失效得很快。可以看到昨天我朋友用这类型因子做的回测图
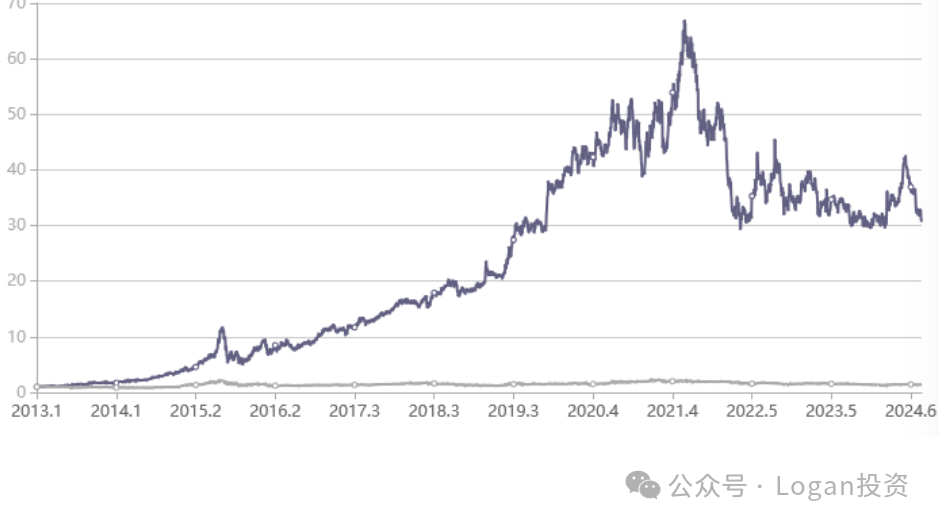
在21年下半年以后几乎就是完全失效了,这可能也是大规模假单使得数据失真导致的。
所以在限制了高频交易的未来,我觉得可以考虑去跟踪一下基于委买委卖计算的因子的表现,就如下文要讲到的集成订单流不平衡因子。
当时我朋友持反对的观点,也给出了上图的回测图,有一定道理。如果有其他观点的欢迎进群交流,我比较喜欢接纳不同的观点,有其他不同的声音那可是好事。
反正最后对于限制高频交易的影响,我交流群里分析就几个:
①利好中低频,利好适合中低频的Veighna框架的推广;
②成交量中枢下移;
③委托量构造的因子更加真实;
④市场波动减少
二、集成订单流不平衡
订单流不平衡概念使用的是Cont(2014)基于买一卖一计算的因子,本质思想是将tick数据整合低频化为分钟级数据。
而在此之后,2023年Cont在Quantitative Finance出了一篇这个因子的续作《Cross-Impact of Order Flow Imbalance in Equity Markets》。
主要是对限价订单簿中的价格档次变化及买卖方向进行细致分析,进而对最优层级和深度层级的订单流不平衡进行独立度量。并在此基础上,对所构建的指标实施标准化处理,以消除不同指标间的量纲影响。最终,采用主成分分析(Principal Component Analysis, PCA)技术,从多层级订单流不平衡指标中提取关键信息,形成综合反映市场动态的订单流不平衡指标。

由于限价订单深度存在日内模式,他们使用了平均规模来衡量相应档位的 OFI,这相当于使用各个层级的订单流不平衡来进行标准化,这样有利于进行多资产间的订单流不平衡的比较。具体公式如下:
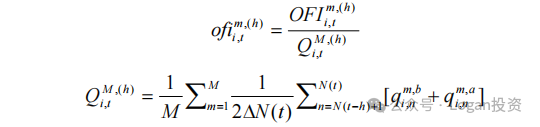

上面的处理就是做标准化。最后会使用PCA对各个档位的ofi 进行PCA降维并提取第一主成分作为因子。而在未发表前的arXiv版本的论文中Cont也写到提取的第一主成分的方差贡献度能达到85%以上,简而言之就是只需要第一主成分就足够有代表性并解释大部分现象了。
Cont在文章中的主要实证并不是去跑因子回测,更多的还是从学术实证的角度去进行线性回归计量分析,去用这个因子去实证各个股票之间的关联性。

每种颜色代表一个行业,可以很清晰的看到行业内各个股票订单流不平衡之间的关联。
所以我就在想,这样不就可以构建知识图谱然后做策略了嘛~
附:各档位订单流不平衡的运作机理
这里得引进交叉冲击的概念。交叉冲击是指标的资产的价格变化收到其他资产订单流的影响。当考虑到其他资产的多层级订单流不平衡,交叉冲击可以拓展到其他资产更加深层级的订单流不平衡对标的资产的价格变化的影响。
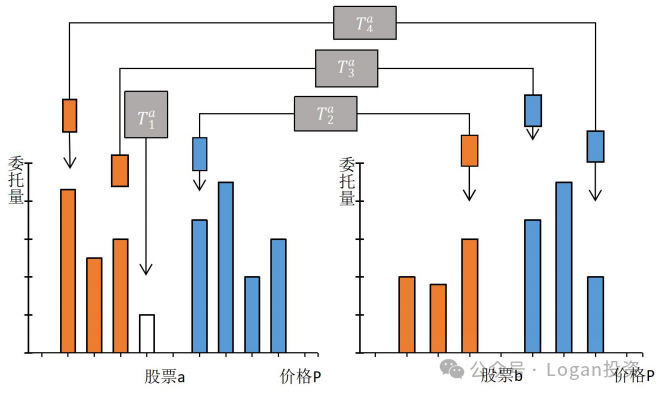
假设目前有股票a和b,股票a上的组合交易策略为T(a1),T(a2)和T(a3),股票b上就是T(b1),T(b2)和T(b3)。股票a的订单流不平衡可以通过一下途径来影响b的价格(Pb)。
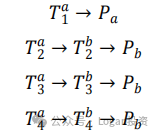
途径1的策略可能是某些高频策略,如微量加价(Penny Jump)高频做市策略,其主要通过限价订单薄的委买价和委卖价的变化来进行双边交易的,属于机构做事策略的一种,本质上是为市场提供流动性,属于订单流不平衡的自冲击。该策略是通过限价订单薄的状态,率先在更有利的价格档位提交订单,影响价格,同时在短时间里获取微小的价差收益。
途径2和3只考虑一级订单流不平衡,可能是配对策略和套利策略。考虑配对策略时,策略1会同时对两只具有高度协整关系的股票的进行双向建仓,即先通过向股票 a 的限价订单薄提交第一档的限价卖单,而后在股票b提交第一档的限价买单进而影响价格。但是途径2忽略了路径4的更深层级的订单流信息。
尽管路径2和3存在上述问题,但是如果能通过提取多层级订单流不平衡的主要信息,那么就可以不用考虑去使用每一档的订单流不平衡来进行建模。如路径4,只要路径4的信息能反映在集成订单流不平衡 ofi 上,那么对于股票b而言就可以用该因子来当作每一层订单流不平衡的统一表征。
总结:这次从更多的维度去考察了订单流不平衡带来的影响并构建了一个因子。文章研究表明,集成订单流不平衡ofi 比仅使用第一档计算的订单流不平衡对价格变动更有解释力。其次文章还在样本外测试了这个因子,证明该因子能带来额外的收益。
import pandas as pd
from tqdm import tqdm
import numpy as np
import rqdatac as rq
from sklearn.decomposition import PCA
from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler
rq.init(account, password)
data = get_price('00001.XSHG', start, end).reset_index(level=0, drop=True)
def multi_imb_En_t(new_row: dict, last_row: dict, level: int = 5):
"""
计算5个level档位的订单流不平衡
"""
Wm = {'bOF1': 0, 'bOF2': 0, 'bOF3': 0, 'bOF4': 0, 'bOF5': 0}
Vm = {'aOF1': 0, 'aOF2': 0, 'aOF3': 0, 'aOF4': 0, 'aOF5': 0}
ask_v_key = ['a1_v', 'a2_v', 'a3_v', 'a4_v', 'a5_v']
bid_v_key = ['b1_v', 'b2_v', 'b3_v', 'b4_v', 'b5_v']
ask_p_key = ['a1', 'a2', 'a3', 'a4', 'a5']
bid_p_key = ['b1', 'b2', 'b3', 'b4', 'b5']
for i in range(0, level):
if new_row[bid_p_key[i]] > last_row[bid_p_key[i]]:
Wm[f'bOF{i + 1}'] = new_row[bid_v_key[i]]
elif new_row[bid_p_key[i]] == last_row[bid_p_key[i]]:
Wm[f'bOF{i + 1}'] = new_row[bid_v_key[i]] - last_row[bid_v_key[i]]
else:
Wm[f'bOF{i + 1}'] = -last_row[bid_v_key[i]]
if new_row[ask_p_key[i]] > last_row[ask_p_key[i]]:
Vm[f'aOF{i + 1}'] = -last_row[ask_v_key[i]]
elif new_row[ask_p_key[i]] == last_row[ask_p_key[i]]:
Vm[f'aOF{i + 1}'] = new_row[ask_v_key[i]] - last_row[ask_v_key[i]]
else:
Vm[f'aOF{i + 1}'] = new_row[ask_v_key[i]]
# En = {f'En{k}': Wm[k] - Vm[k] for k in Wm}
return Wm, Vm
def generate_data(data: pd.DataFrame):
G_data = {}
cal_footpoint_model = 'quota_method'
last_row = []
for index, row in tqdm(data.iterrows()):
if not last_row:
last_row = row
G_data[index] = {}
bOF, aOF = multi_imb_En_t(row, last_row)
G_data[index].update(bOF)
G_data[index].update(aOF)
midpoint = (row['a1'] + row['b1']) / 2 # 计算中间价
G_data[index].update({'midprice': midpoint})
last_price = row['last']
sub_data = {}
if cal_footpoint_model == 'quota_method':
if last_price > midpoint:
pre_along = 1
elif last_price < midpoint:
pre_along = -1
else:
pre_along = pre_along
sub_data['dirc'] = pre_along
if cal_footpoint_model == 'quota_method':
sub_data['OIBSH'] = pre_along * (max(0, row['volume'] - last_row['volume'])) # 股票时用的
# sub_data['OIBNUM'] = pre_along * (row['num_trades'] - last_row['num_trades']) # 米筐的期货数据没有num_trades
sub_data['OIBNUM'] = pre_along # 没有num_trades时只能用每个tick当作一笔交易
sub_data['spread'] = row['a1'] - row['b1']
sub_data['S_B_share'] = max(0, row['volume'] - last_row['volume'])
G_data[index].update(sub_data)
G_data[index].update({'OIBDOL': pre_along * (max(0, row['total_turnover'] - last_row['total_turnover']))})
G_data[index].update({'last_volume': max(0, row['volume'] - last_row['volume'])}) # 股票时用的
last_row = row.to_dict()
G_data = pd.DataFrame(G_data).T
new_data = data.join(G_data)
return new_data
def generate_target_freq_train_data(data: pd.DataFrame, freq: str):
"""
:param freq 填入resample的频率 1min 15min 1D 等
"""
freq = freq
data['event_count'] = 1
data['close'] = data['last']
data['high'] = data['last']
data['low'] = data['last']
data['open'] = data['last']
x = data.resample(freq
).agg({'close': 'last', 'high': 'max', 'low': 'min', 'open': 'first',
'OIBSH': 'sum', 'OIBNUM': 'sum', 'OIBDOL': 'sum',
'spread': 'mean',
'last': 'last', 'midprice': 'last',
'last_volume': 'sum',
'S_B_share': 'sum',
'aOF1': 'sum', 'aOF2': 'sum', 'aOF3': 'sum', 'aOF4': 'sum', 'aOF5': 'sum',
'bOF1': 'sum', 'bOF2': 'sum', 'bOF3': 'sum', 'bOF4': 'sum', 'bOF5': 'sum',
'a1_v': 'sum', 'a2_v': 'sum', 'a3_v': 'sum', 'a4_v': 'sum', 'a5_v': 'sum',
'b1_v': 'sum', 'b2_v': 'sum', 'b3_v': 'sum', 'b4_v': 'sum', 'b5_v': 'sum',
'dirc': 'sum', 'event_count': 'sum'
}).rename(columns={'last_volume': 'volume'})
x['B-S/(BS)'] = x['OIBSH'] / x['S_B_share']
x = x.loc[~(x == 0).all(axis=1)]
x.dropna(inplace=True)
x['returns'] = np.log(x['midprice']) - np.log(x['midprice'].shift(1))
x['midprice_delta'] = x['midprice'] - x['midprice'].shift(1)
x['OFI1'] = x['bOF1'] - x['aOF1']
x['OFI2'] = x['bOF2'] - x['aOF2']
x['OFI3'] = x['bOF3'] - x['aOF3']
x['OFI4'] = x['bOF4'] - x['aOF4']
x['OFI5'] = x['bOF5'] - x['aOF5']
M = 5
Q1 = (x['a1_v'] + x['b1_v']) / 2 / x['event_count']
Q2 = (x['a2_v'] + x['b2_v']) / 2 / x['event_count']
Q3 = (x['a3_v'] + x['b3_v']) / 2 / x['event_count']
Q4 = (x['a4_v'] + x['b4_v']) / 2 / x['event_count']
Q5 = (x['a5_v'] + x['b5_v']) / 2 / x['event_count']
Qm = (Q1 + Q2 + Q3 + Q4 + Q5) / M
x['ofi1'] = x['OFI1'] / Qm
x['ofi2'] = x['OFI2'] / Qm
x['ofi3'] = x['OFI3'] / Qm
x['ofi4'] = x['OFI4'] / Qm
x['ofi5'] = x['OFI5'] / Qm
# x.dropna(inplace=True)
x = x[~x.isin([np.nan, np.inf, -np.inf]).any(1)]
X = x[['ofi1', 'ofi2', 'ofi3', 'ofi4', 'ofi5']]
pca = PCA(n_components=1)
X_pca = pca.fit_transform(X)
ofiI = pd.Series(X_pca.flatten(), index=X.index)
standard_scaler = StandardScaler()
ofiI_standard = standard_scaler.fit_transform(np.array(ofiI).reshape(-1, 1))
x['ofiI'] = pd.Series(ofiI_standard.flatten(), index=X.index)
return x
bb = generate_data(data.iloc[:1000])
dd = generate_target_freq_train_data(bb,'1min')
dd
"""
ofiI既是所计算的集成订单流不平衡因子
"""
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(20, 10))
ax.plot(dd.close, label='close')
ax2 = ax.twinx()
ax2.plot(dd.ofiI, color='r', label='ofiI')
ax.legend(fontsize=25,loc='upper left')
ax2.legend(fontsize=25, loc='upper right')
ax2.axhline(0, color='y', linestyle='--')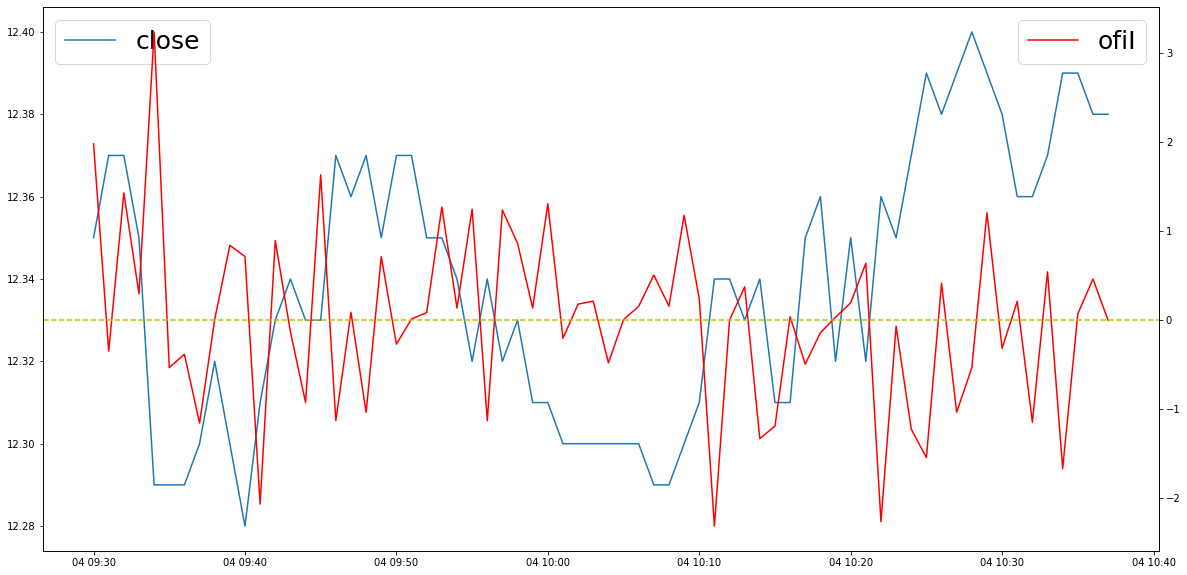
想要论文pdf和因子计算完整代码的朋友可以在公众号(Logan投资)后台回复“20240727”即可。




