该主题文章来源于公众号：Logan投资

上次去深圳参加咱们Veighna开源举办的分享会，听了陈总的分享，会中的一些关于因子统计再构建的感悟文章《最近思考的量化指标再挖掘》我分享在了公众号中，欢迎大家关注和交流。

本帖子主要是分享关于加速RSRS计算的方法，改进后的代码比原版快了150倍左右，而且计算结果完全一致。

RSRS指标是基于光大证券研报《基于阻力支撑相对强度(RSRS)的市场择时》，给出了RSRS斜率指标择时，以及在斜率基础上的标准化指标择时策略。

阻力支撑相对强度(Resistance Support Relative Strength, RSRS)是另一种阻力位与支撑位的运用方式，它不再把阻力位与支撑位当做一个定值，而是看做一个变量，反应了交易者对目前市场状态顶底的一种预期判断。

其他因子的逻辑不多介绍了，大家可以去看这里
知乎的文章：https://zhuanlan.zhihu.com/p/33501881
原始RSRS计算代码如下：

import rqdatac as rq
from tqdm import tqdm
rq.init('账号', '密码')
data = rq.get_price('510330.XSHG', '2023-01-01','2024-01-01', frequency='30m')
​
def RSRS(low,high, regress_window: int,
         zscore_window: int, array: bool = False)
:
    """
    :param
    """
​
    high_array = high
    low_array = low
​
    highs = copy.deepcopy(high_array)
    lows = copy.deepcopy(low_array)
    rsrs_beta = []
    rsrs_rightdev = []
    zscore_rightdev = []
​
    N = regress_window
    M = zscore_window
​
    for i in range(len(highs)):
        try:
            data_high = highs[i - N + 1:i + 1]
            data_low = lows[i - N + 1:i + 1]
            X = sm.add_constant(data_low)
            model = sm.OLS(data_high, X)
​
            results = model.fit()
            beta = results.params[1]
            r2 = results.rsquared
​
            rsrs_beta.append(beta)
            rsrs_rightdev.append(r2)
​
            if len(rsrs_beta) < M:
                zscore_rightdev.append(0)
            else:
                section = rsrs_beta[-M:]
                mu = np.mean(section)
                sigma = np.std(section)
                zscore = (section[-1] - mu) / sigma
                # 计算右偏RSRS标准分
                zscore_rightdev.append(zscore * beta * r2)
​
        except:
            rsrs_beta.append(0)
            rsrs_rightdev.append(0)
            zscore_rightdev.append(0)
​
    if array:
        return zscore_rightdev
    else:
        return zscore_rightdev[-1]
test = []
for i in tqdm(range(10)):
    start = time.time()
    ddaa = RSRS(data.low, data.high, 18, 600,array=True)
    end = time.time()
    t = end - start
    test.append(t)
print(f'原始rsrs代码运行平均用时：{np.mean(test)}')

根据网上的代码，用原始的代码计算RSRS并记录运行了10次的平均运算时间。

可以看到用原始代码运行的话平均需要7.89秒（参数为N=18,M=600）

这是仅对于一个股票计算的，若是根据RSRS在3000只票里选股就要计算很多次，进而花费时间大概是6.575个小时，这对于日频策略来说也够呛了，对于高频一点的策略或者平时的因子分析研究中更不用说了，还是很耗费时间的。

所以接下来上神器，numpy！
思想是用numpy矩阵运算实现滚动窗口的批量线性回归和指标计算。代码如下：

import numpy as np
​
from numpy.lib.stride_tricks import as_strided as strided
​
def rolling_window(a:np.array, window: int):
    '生成滚动窗口，以三维数组的形式展示'
    shape = a.shape[:-1] + (a.shape[-1] - window + 1, window)
    strides = a.strides + (a.strides[-1],)
    return strided(a, shape=shape, strides=strides)
​
def numpy_rolling_regress(x1, y1, window: int=18, array: bool=False):
    '在滚动窗口内进行，每个矩阵对应进行回归'
    x_series = np.array(x1)
    y_series = np.array(y1)
    # 创建一个一维数组
    dd = x_series
    x = rolling_window(dd, window)
    yT = rolling_window(y_series, window)
    y = np.array([i.reshape(window, 1) for i in yT])
    ones_vector = np.ones((1, x.shape[1]))
    XT = np.stack([np.vstack([ones_vector, row]) for row in x])  #加入常数项
    X = np.array([matrix.T for matrix in XT])  #以行数组表示
    reg_result = np.linalg.pinv(XT @ X) @ XT @ y   #线性回归公示
​
    if array:
        return reg_result
    else:
        frame = pd.DataFrame()
        result_const = np.zeros(x_series.shape[0])
        const = reg_result.reshape(-1, 2)[:,0]
        result_const[-const.shape[0]:] = const
        frame['const'] = result_const
        frame.index = x1.index
        for i in range(1, reg_result.shape[1]):
​
            result = np.zeros(x_series.shape[0])
            beta = reg_result.reshape(-1, 2)[:,i]
            result[-beta.shape[0]:] = beta
            frame[f'factor{i}'] = result
        return frame
​
def numpy_rsrs(low:pd.Series, high:pd.Series, N:int=18, M:int=600):
    beta_series = numpy_rolling_regress(low, high, window=N, array=True)
    beta = beta_series.reshape(-1, 2)[:,1]
​
    beta_rollwindow = rolling_window(beta, M)
    beta_mean = np.mean(beta_rollwindow, axis=1)
    beta_std = np.std(beta_rollwindow, axis=1)
    zscore = (beta[M-1:] - beta_mean) / beta_std
    return zscore
​
test = []
for i in tqdm(range(50)):
    start = time.time()
    numpy_rsrs(data.low, data.high)
    end = time.time()
    test.append(end - start)
print(f'numpy加速后的rsrs代码运行平均用时：{np.mean(test)}')

这里的RSRS没有进行右偏处理，右偏RSRS在下文中。
运行了50次的平均用时

可以看到平均运行了约0.05秒，足足快了157.8倍！！！！！
这个速度可能还不足以满足几千只股票的RSRS指标的计算，但是对于研究已经是极大的提速了。若限制1秒以内的延迟上限，再用上多进程multiprocessing，只能满足20~100只标的的RSRS指标的计算，但这也满足宽基指数或者股指期货的分钟级和小时级的择时策略了。
进阶一点就是考虑用DASK框架写成并发过程，用这个函数并发计算几千只股票的因子。

具体速度得看各位的电脑配置了，我就是个小小的破surface pro，16G内存。

以上是RSRS计算的代码和过程。
而原版RSRS中还对其进行修正为RSRS右偏标准分，而我也复现了出来，搞了好一会儿的高等数学和线性代数。具体运行时间如下，为了减少rolling次数，所以我全部都写在了同一个函数里面。为了展示运行结果的正确性，我挑出numpy加速后的RSRS右偏标准分最后100条数据和原始代码计算的RSRS右偏标准分进行了对比

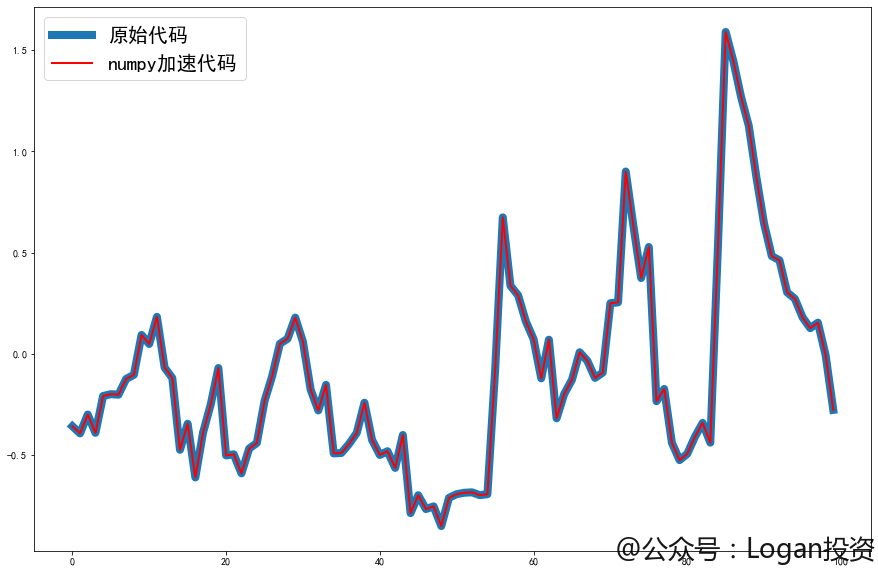
蓝色粗线为原始的，覆盖在上面的红色细线是numpy进行计算的。可以看到完全一致，计算结果无误。
最后附上回测图，RSRS右偏标准分择时指标在近年回撤得比较厉害。

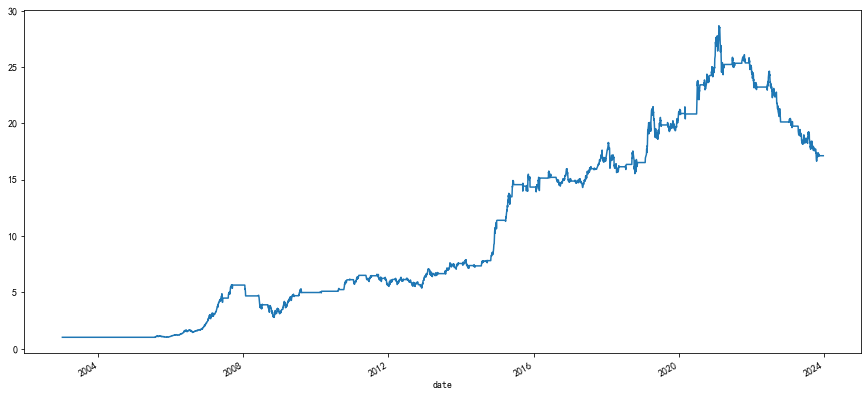
RSRS右偏标准分的代码有需要的朋友可以在关注公众号后再后台私信我“RSRS”即可。

这个加速效果相当不错啊，帮你加个精华

感谢陈总，那我直接分享全部代码，给咱们社区的福利吧

import warnings
from tqdm import tqdm
warnings.filterwarnings('ignore')

def numpy_cal_r2(x:np.array, yT:np.array,
                 beta: np.array, const:np.array):
    y_predict = x * beta.reshape(-1, 1) + const.reshape(-1, 1)
    # mse = np.mean((yT - y_predict) ** 2, axis=1)
    #
    # # 计算均方根误差（RMSE）
    # rmse = np.sqrt(mse)
    #
    # # 计算平均绝对误差（MAE）
    # mae = np.mean(np.abs(yT - y_predict), axis=1)

    # 计算决定系数（R-squared, R^2）
    # 首先计算总平方和
    total_ss = np.sum((yT - np.mean(y_predict, axis=1).reshape(-1, 1)) ** 2, axis=1)
    # 然后计算回归平方和
    residual_ss = np.sum((yT - y_predict) ** 2, axis=1)
    r_squared = 1 - (residual_ss / total_ss)
    return r_squared

def numpy_rsrs_rightrev(x1, y1, N_window: int=18, M_window: int = 600, array:bool=True):
    x_series = np.array(x1)
    y_series = np.array(y1)
    # 创建一个一维数组
    dd = x_series
    x = rolling_window(dd, N_window)
    yT = rolling_window(y_series, N_window)
    y = np.array([i.reshape(N_window, 1) for i in yT])
    ones_vector = np.ones((1, x.shape[1]))
    XT = np.stack([np.vstack([ones_vector, row]) for row in x])  #加入常数项
    X = np.array([matrix.T for matrix in XT])  #以行数组表示
    reg_result = np.linalg.pinv(XT @ X) @ XT @ y   #线性回归公式

    beta = reg_result.reshape(-1, 2)[:,1]
    const = reg_result.reshape(-1, 2)[:,0]
    r_squared = numpy_cal_r2(x, yT, beta, const)

    beta_rollwindow = rolling_window(beta, M_window)
    beta_mean = np.mean(beta_rollwindow, axis=1)
    beta_std = np.std(beta_rollwindow, axis=1)

    zscore = (beta[M_window - 1:] - beta_mean ) / beta_std

    period_len = zscore.shape[0]
    zscore_rightdev = zscore * r_squared[-period_len:] * beta[-period_len:]

    if array:
        return zscore_rightdev
    else:
        zz = np.zeros(len(x1))
        zz[-zscore_rightdev.shape[0]:] = zscore_rightdev
        zz = pd.Series(zz, index=x1.index)
        return zz


test = []
for i in tqdm(range(50)):
    start = time.time()
    rsrs_rightrev = numpy_rsrs_rightrev(data.low, data.high, array=False)
    end = time.time()
    t = end - start
    test.append(t)
print(f'numpy加速后rsrs右偏标准分代码运行平均用时：{np.mean(test)}')

不错干活满满，试了一下完全用的上！