什么是对数化处理

我们平时看到的K线图几乎都是采用普通坐标 ，而有一种叫作对数坐标的K线图大部分人可能没了解过。

在介绍对数坐标下的K线图之前，我们先思考一个问题：以下两种情形，情形1的涨幅大还是情形2的涨幅大？

• 情形1：从100点涨到1300点
• 情形2：从1000点涨到6000点

从绝对数值来看，情形1涨了1200点（1200=1300-100），情形2涨了5000点（5000=6000-1000）。情形2涨的绝对幅度大。

但如果换个新的思路呢？以收益率的角度看，结果完全反过来了：情形1涨了12倍(12=(1300-100)/100)，情形2涨了5倍(5=(6000-1000)/1000)。情形1的收益率更大。

从实际情况，我们也应该更看重价格收益率而非价格涨幅度。回归现实世界中的例子，情形1对应的是中国股市刚开始时期上证指数行情（91-92年），若投入1000元，那么期末收益为12000元。情形2对应的是06-07年牛市行情，同样投入1000元，期末收益为5000元。

所以，从收益率上就凸显了对数化坐标的优势：

1. 易于处理不同价量变化的关系：贵州茅台从8000涨到16000的收益率与中国平安从60涨到120的收益率是一样的。
2. 对数收益率考虑到复利因数，故曲线相对平滑，平滑的时间序列更利于直接观察收益率和进行数据分析。
3. 对数收益率具有可加性，它的均值可以正确反映出的真实收益率：如一个投资产品，今年涨10%，明年跌10%，从算术平均角度看是不赚不亏，但是其产品净值以下降到0.99（0.99= 11.10.9）。而对数收益率可以解决这个痛点。

下面2幅图分别对应上证指数的标准坐标和对数坐标。显然，对数坐标能更容易挖掘到盈利点。

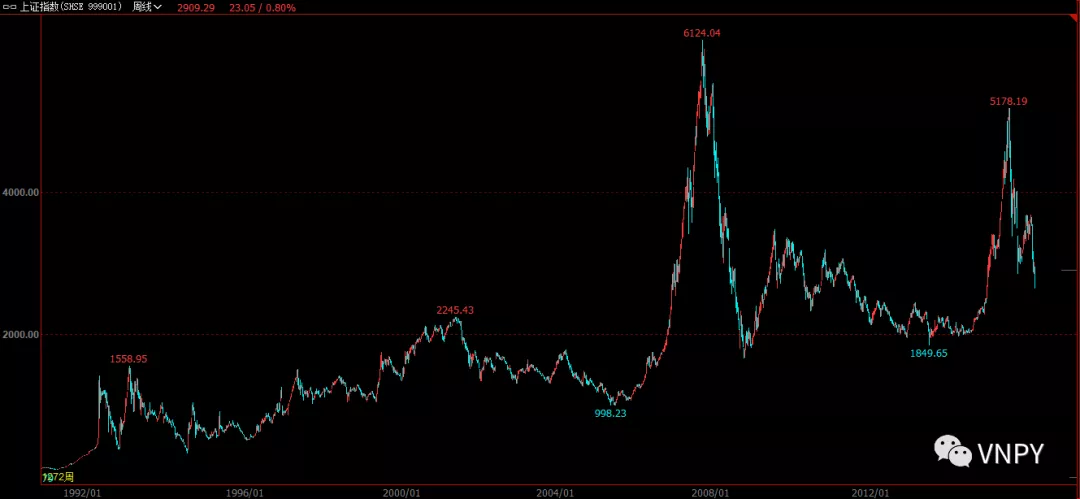
（标准坐标）

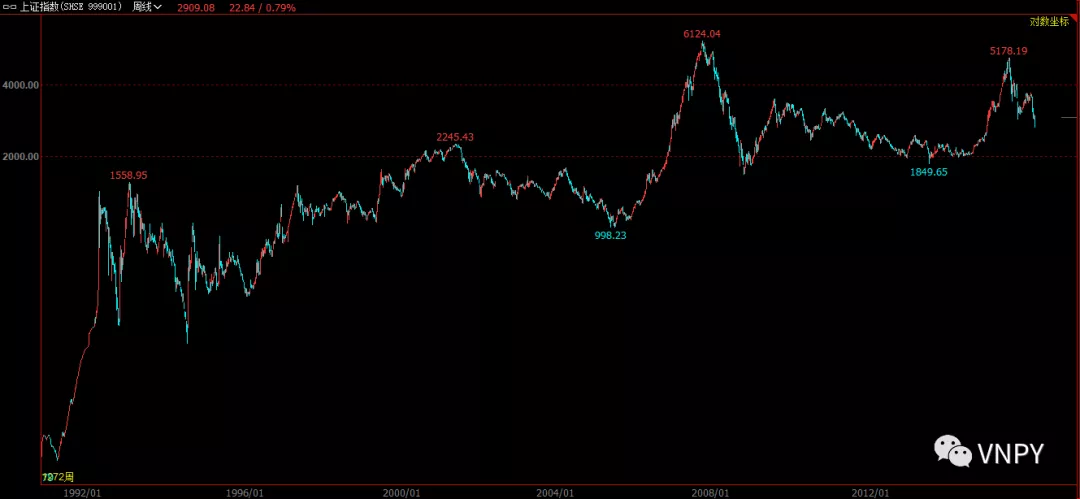
（对数坐标）

对数化指标的适用领域

CTA策略大致可以分成2类：

1）趋势突破类

行情一旦有突破迹象（即行情还未走远或者正式确立）就下单成交，但是实际上大部分的突破都是假的，只有少部分行情能走到一波比较强的趋势。所以趋势突破类策略具有胜率低的特点（一般预测准确率< 40%)。

策略的盈利主要依赖对止盈止损的控制：如亏损的交易止损设为10%，而少部分盈利的交易止盈设为500%。若交易次数足够多（满足大数定律和中心极限定理），那么少部分能捕捉到大趋势的盈利，足以覆盖大部分假突破导致的风险，从而让策略整体盈利。

若胜率在30%到40%，那么盈亏比需要控制在2以上，从而使整个策略是盈利的。举个例子来简单说明一下：
 

• 胜率40%，代表40%预测方向对的，60%预测方向错误的；
• 盈亏比2，代表在对的交易上，盈利是2，在错误的交易上，亏损是1；
• 综合起来，总体盈利为0.8（0.8=40% x 2），总体亏损为0.6（0.6=60% x 1），那么利润为0.2（0.2=0.8-0.6）

低胜率与高盈亏比是趋势突破类策略的两大特征，在统计学上表现出尖峰肥尾的特点，尖峰代表亏损的交易比较多，但亏损数额都不大，肥尾则说明少部分成功交易所带来的盈利是巨大的。
 

趋势突破类中的突破通常指的是通道突破，如突破布林带通道的上轨做多，突破布林带通道下轨做空。
 

• 布林带通道上轨 = 收盘价均线 + N x 收盘价标准差
• 布林带通道下轨 = 收盘价均线 - N x 收盘价标准差

由于布林带通道的构成因素是基于标准坐标的，属于价位指标。对数化的效果反而不好，所以对数化的技术不适用于趋势突破类策略。

2）趋势跟踪类

行情已经突破并且走了有一段距离（即行情正式确立）才下单成交。因为行情已经确立，所以策略预测的成功率会比较高；但由于行情已经走出一段距离才下单追上去，盈利空间大幅度减少，甚至会遇到行情的反转。

所以，趋势跟踪类策略的特点恰好与趋势突破类相反：胜率高，盈亏比低。它所依赖的不是基于绝对价位的通道类突破，而是一些非价位指标，如RSI指标高于66时候做多，RSI指标低于34时做空等。

对数化处理非价位指标，可以进一步提升趋势跟踪类策略的盈利空间，下面通过vn.py里面的AtrRsi策略来展示对数化的效果。
 
 

以AtrRsiStrategy为例

策略的原理

行情能走出大趋势的充分条件是波动率增大，即当前波动率突破历史平均波动率（ATR>ATR均值）。在波动率变大，市场参与者增多或者多空双方开始发力的时候，我们可以判断在一定时间内：

• 若收盘价的平均涨幅要大于跌幅（如RSI>66），说明多头已取得上风，并且多头趋势还会持续下去，可以去做多。
• 若收盘价的平均跌幅幅要大于涨幅（如RSI<34），说明空头已取得上风，并且空头趋势还将持续下去，可以去做空。

然后我们看看原始的策略效果如何？

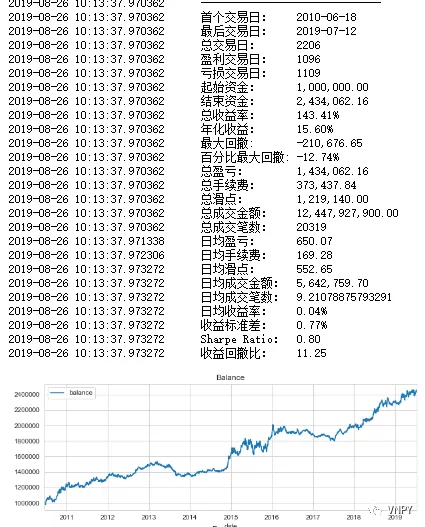
策略的夏普比率是0.8，收益回撤比是11.25。

尝试对数化非价位指标

vnpy\vnpy\trader目录下的utility.py文件是负责定义技术指标的。这些技术指标都是基于talib库来实现的，在log字段填True，就可以对数化我们需要的非价位指标了。

    def atr(self, n, log=False, array=False):
        """
        Average True Range (ATR).
        """
        if log:
            result = talib.ATR(np.log(self.high), np.log(self.low), np.log(self.close), n)
        else:
            result = talib.ATR(self.high, self.low, self.close, n)

        if array:
            return result
        return result[-1]

    def rsi(self, n, log=False, array=False):
        """
        Relative Strenght Index (RSI).
        """
        if log:
            result = talib.RSI(self.close, n)
        else:
            result = talib.RSI(np.log(self.close), n)
        if array:
            return result
        return result[-1]

在新的AtrRsi策略上，通过对数化处理的ATR和RSI指标，我们看看回测效果。

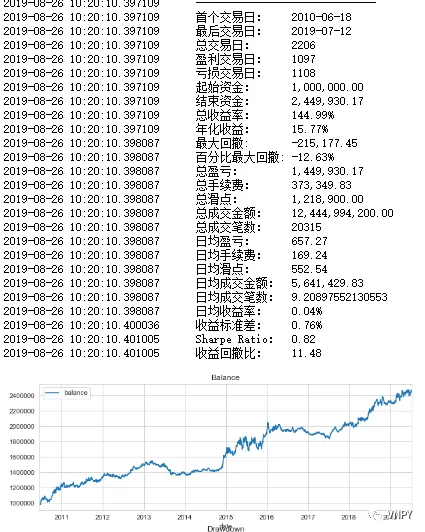
夏普比率是0.82，收益回撤比为11.48。对数化非价位指标对策略有影响，但是效果甚微。

 
 
进一步验证：参数优化

为了进一步验证对数化非价位指标对策略有没有效果，我们用到了参数优化：优化目标是最大化收益回撤比，优化的参数分别是atr_length、atr_ma_length、rsi_length。
 

setting = OptimizationSetting()
setting.set_target("return_drawdown_ratio")
setting.add_parameter("atr_length", 18,24, 2)
setting.add_parameter("atr_ma_length",8, 12,2)
setting.add_parameter("rsi_length",3,7,2)
engine.run_optimization(setting)

我们先把对数化技术指标的策略称之为实验组，原始策略称之为对照组。优化完毕后，实验组和对照组最优参数都相同，均为：

atr_length=18

atr_ma_length=12,

rsi_length=5

但是，实验组的收益回撤比整体要高于对照组的。
 

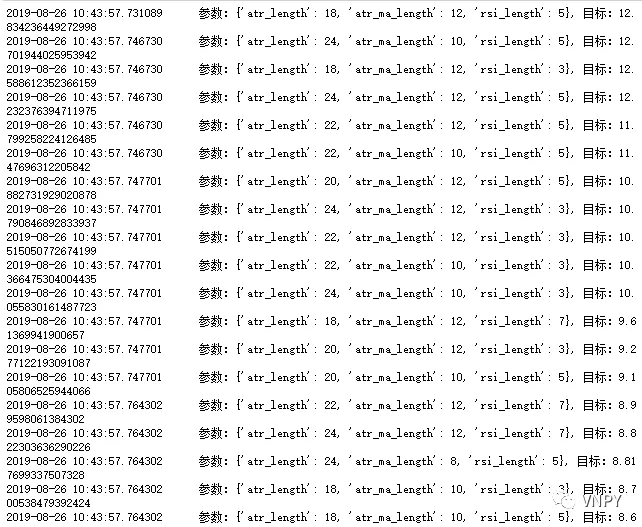
（实验组优化结果）

（对照组优化结果）
 

选取最优参数，我们再跑一下策略回测，就可以看到对数化非价位指标的确适用于趋势跟踪类策略的了。

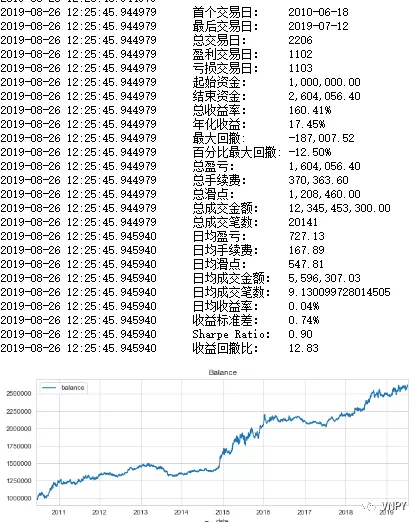
（实验组最优参数回测）

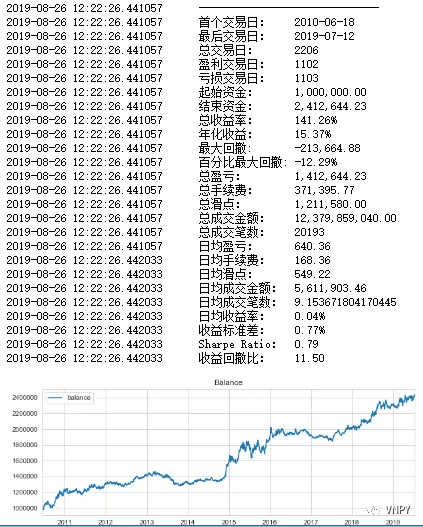
（对照组最优参数回测）

《vn.py全实战进阶》课程全新上线，一共50节内容覆盖从策略设计开发、参数回测优化，到最终实盘自动交易的完整CTA量化业务流程，目前已经更新到第八集，详细内容请戳课程上线：《vn.py全实战进阶》！

 
了解更多知识，请关注vn.py社区公众号。

mark