最近在看一本友人推荐的陈博士的《算法交易: 致胜策略和原理》一书,虽然书名很神棍,其实内容是很实际结合理论的,不少内容击中了我现在困惑的痛点。
本文是学习书中《1.3 统计学在回测程序上的应用:假设检验》一节的理解,对概率论很久没研究,如果理解错误请指教。
在交易策略设计优化完成后,都会放入一个测试集进行回测,但是不论怎么样收集,用于回测的数据集是始终是有限的,而且,无论我们计算的统计指标是什么,诸如平均收益率,还有最大跌幅等,它们都具有随机性。有时候往往很困惑,就是在相对于无尽市场交易数据,那些一段时间小样本回测结果能说明说明呢。
嗯,其实统计学家已经开发了一种通用的方法,即假设检验,用以实现前述的目标。
关于假设检验是一个非常大的课题,有兴趣可以去看看相关书籍或知乎,我这边举个例子。
有个说现在高中生营养上来,身高也高了,平均有1.75了。那么这个说法是一个假设,怎么检验了,当然把所有高中生拉出来量身高一平均最好,但是不现实。我们把最近高中的学生请出来做一个小样本测量,发现300名高中生的平均身高是1.65,相对于1.75这个假设可能有问题。但是可能是单个小概率时间,这个时候我们加入另外一个指标标准差,通常身高是按照正态概率分布的,按照标准正态分布函数,如果标准差是0.05米的话;得出1.65相对于1.75是两个标准差sigma,可以查标准正态分布概率表,1.65发生的概率差不多是2.2%这样概率。
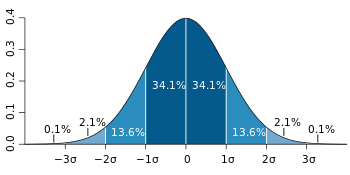
这里的2.2%统计学叫做p-value显著水平,通常在p-value < 0.05我们可以拒绝假设,就有理由怀疑假设高中生平均身高的正确性。当然还有一个情况,就是平均高中生真的1.75,但是我们边上这个校园食堂有克扣,这个就是发现特殊情况,这个通常用在次品抽样检测中。
当然300个这个检测点数也很重要,越大越好,不然光量一个高中生是说明不了问题,这里为了简化分析,把样本视作一个人。
好了回到回测结果分析的时候,具体地讲,应用于回测系统当中的假设检验之基本框架遵循如下的几个步骤:
(1)基于某个有限的样本数据的回测系统,我们需要计算一个特定的统计测度值,我们称之为假设检验统计量,比如最大收益,最大回测一类。具体地讲,通常情况下,假设检验统计量就是在一定时间序列内,某个特定交易策略相关的日平均收益率。
(2)我们设定基于无限系列数据而生成的真实日间平均收益率为零,此种前提条件被称之为“零假设”。
(3)我们设定日间收益率的概率分布是已知的,即基于“零假设”的理念,相应概率分布的均值为零。接下来,我们就要阐述如何确定此种概率分布。
(4)基于零假设的概率分布理念,我们设定:平均日间收益率至少不能低于回测系统中的观测值——对此概率,我们用p来表示(对于一般的检验统计来说,在极端情况下,检验统计所对应的概率可能出现负值的情况)。我们将概率p称为假定值,如果p值极小(比如小于0.01),那就意味着我们可以“拒绝零假设”,同时,从统计意义上讲,回测系统中的收益会显现得非常明显。
上面是书本原文,比较书面,简单来说,
1)就是用日平均收益作为测量指标,就和上面身高一样;
2)同时假定真实日平均收益率为0,就和上面假定平均身高1.75;
3)日平均收益率是按照概率分布,这个采用正态分布(0,1),标准差用样本集的标准差,
4) 求出策略回测日收益相对于假设的p-value显著水平,如果p-value小于0.01,意味则从统计意义上说,策略相对有特殊性,获得的收益并不是普通概率事件,其实就是我们经常用的一个数值,后面透露。
下面先简单看看为什么真实日平均收益率为0,之前对数收益率一文提到的“中心极限定理”和“大数定律”,这里不具体分析。就是读取2012年到现在螺纹钢价格指数走势,第一行是对数价格,第二行是每日收益率,最后是收益率的按数量排列,是一个近似的正态分布。
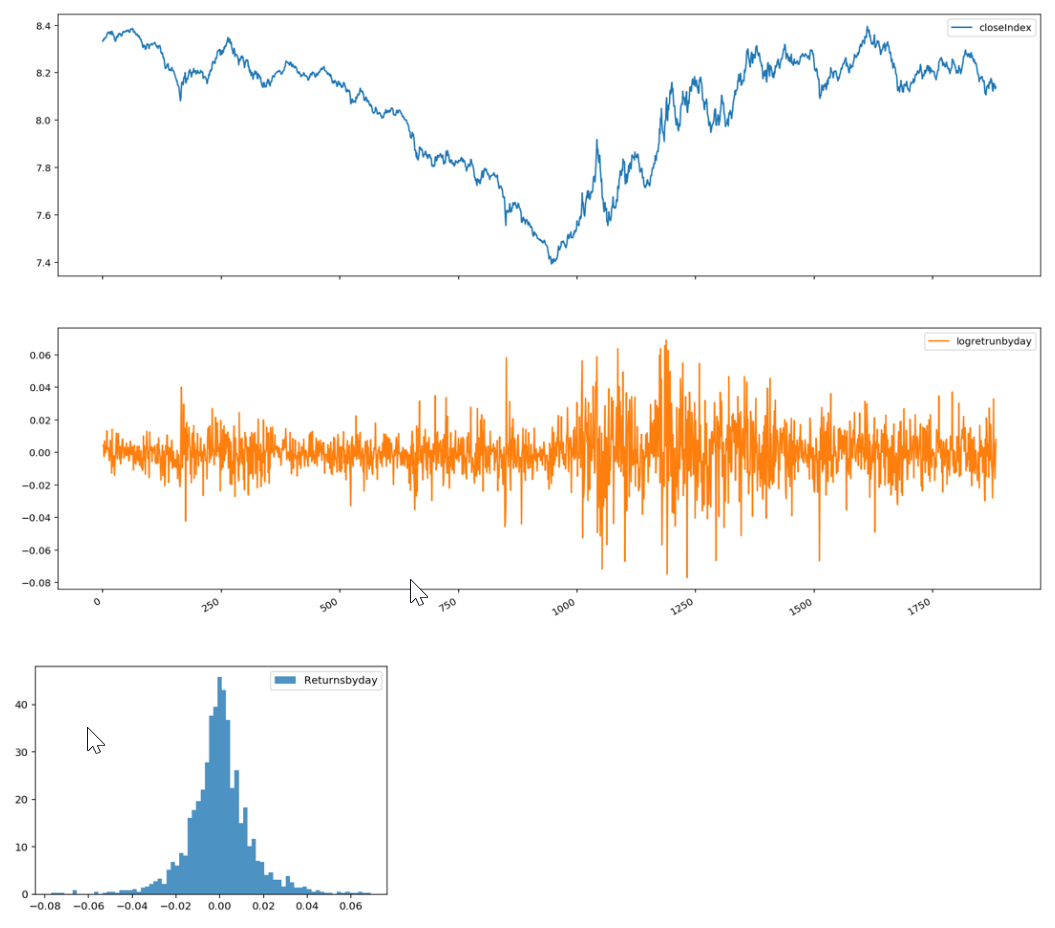
求出来按日平均收益率: -0.00010227409878337288,收益率标准差: 0.014829529492971772。其他股票,基金大多如此。
那么按照假设日平均收益率为0,从回测结果知道平均日收率为MEAN(dailyreturn),同时用样本集的标准差STD(dailyreturn),我们要求出p-value。 其实就是 (MEAN(dailyreturn) - 0)/ STD(dailyreturn) , 求出相对是多少标准差sigma,查表得出对应发生概率值。
眼熟的就会发现 这个不就是夏普指标(Sharpe Ratio) MEAN(dailyreturn) / STD(dailyreturn) , 还真是。这是因为按照高斯分布的相关理念,标准统计检验量正是均值除以标准差,再乘以相应点数的平方根。
考虑到采样点数, 标准化的统计检验数值 为 MEAN(dailyreturn) / STD(dailyreturn) *sqrt(DayNumber)
这个也是VNPY回测夏普值的计算方法,不过使用252日,我在想是不是应该改成totalDays更好
sharpeRatio = dailyReturn / returnStd * np.sqrt(annualDays)
最后,比如回测夏普值是1.65以上,说明这个策略不是随机概率事件。
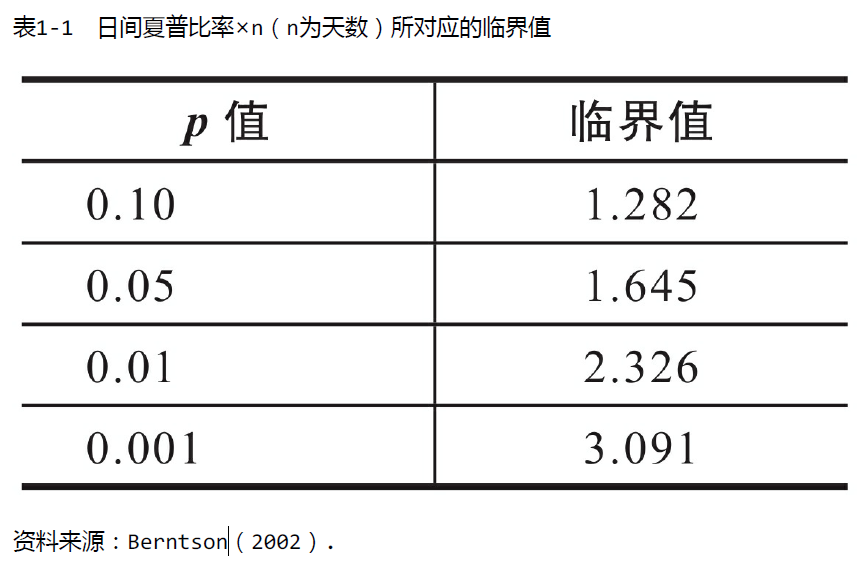
上述假设检验的方法,发现和我们优化策略理念是一致的,而且追求高夏普比率的策略在统计学的意义上具有更加明显的效果。
最后原文还用另外两种方法,蒙特卡洛模拟价格和系列模拟交易来一起分析,有兴趣可见原书。


