OptionMaster - 期权波动率交易模块¶
功能简介¶
OptionMaster是用于期权波动率交易的功能模块,用户可以通过OptionMaster完成期权实时定价、波动率曲面跟踪、持仓希腊值监控、组合压力测试、电子眼自动交易等功能。
加载启动¶
VeighNa Station加载¶
启动登录VeighNa Station后,点击【交易】按钮,在配置对话框中的【应用模块】栏勾选【OptionMaster】。
脚本加载¶
在启动脚本中添加如下代码:
# 写在顶部
from vnpy_optionmaster import OptionMasterApp
# 写在创建main_engine对象后
main_engine.add_app(OptionMasterApp)
配置组合¶
在管理界面上,选择要交易的期权产品,点击【配置】按钮打开如下图所示的组合配置对话框:
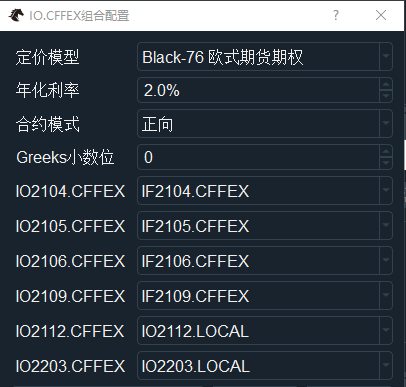
配置参数如下:
定价模型
Black-76模型:针对欧式期货期权(股指期权);
Black-Scholes模型:针对欧式股票期权(ETF期权);
Binomial-Tree模型:针对美式期货期权(商品期权);
年化利率
定价模型中用到的无风险折现利率;
合约模式
正向:包括ETF期权、期货期权、股指期权等大多数产品;
Greeks小数位
显示希腊值时保留的小数位数;
期权链对应的定价标的
注意只有选择了标的物的期权链,才会被加入交易组合;
定价标的物支持
期货合约:交易所本身提供的期货价格;
合成期货:基于期权价格算出的合成期货价格;
OptionMaster在定价计算过程中会对标的物价格相对期权链的升贴水进行自动修正,因此推荐选择交易最活跃的合约作为标的物。
点击底部的【确认】按钮,完成期权组合的初始化,此时管理界面上的【配置】按钮会被锁定,而其他按钮则会被激活。
行情监控¶
点击管理界面的【T型报价】按钮,打开T型报价窗口:
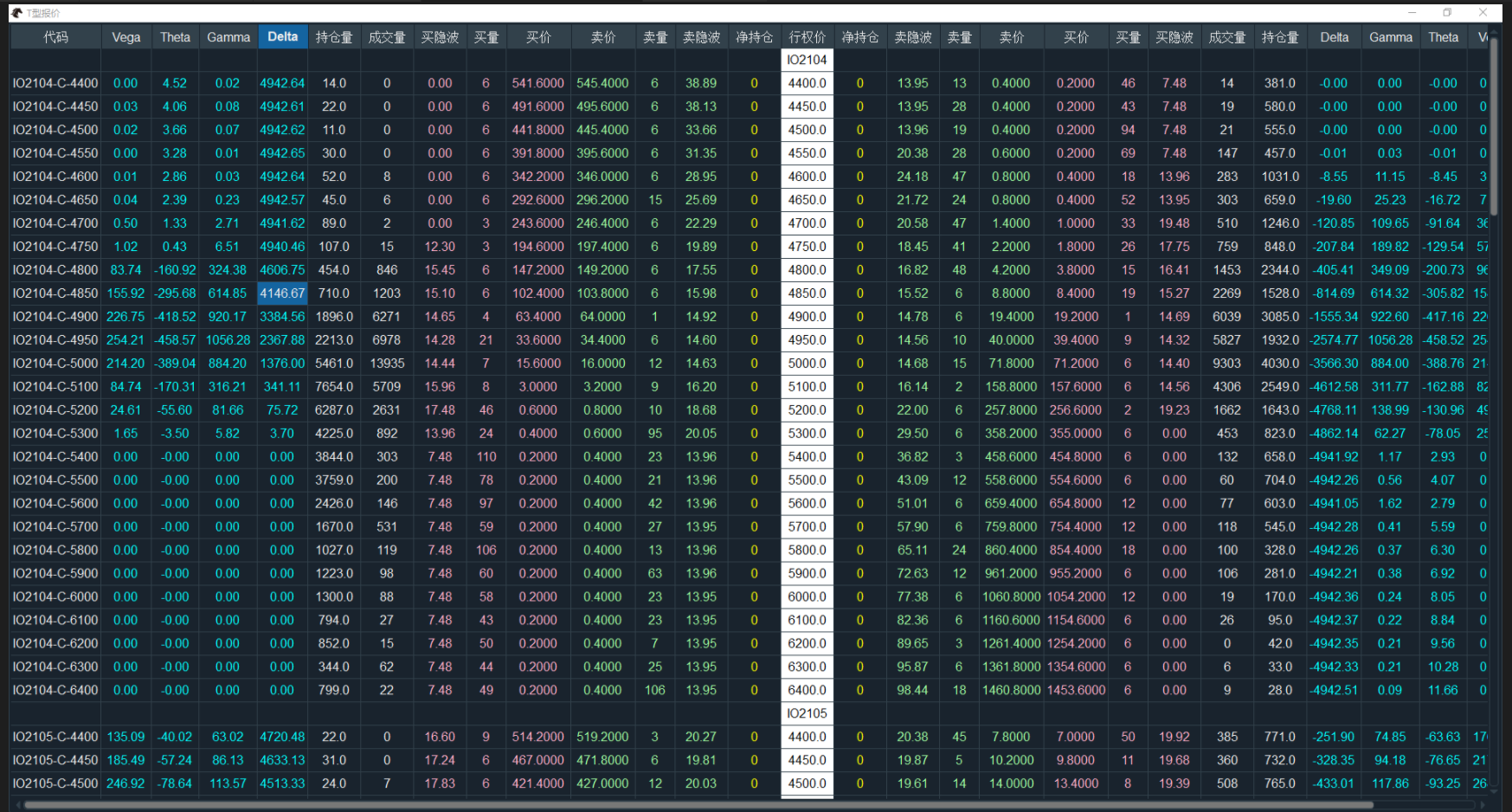
窗口整体分为左右区域,中间白色列为行权价,左侧为看涨期权,右侧为看跌期权。
每行显示的为某一行权价期权对应的信息,从外向内显示的信息包括:
合约代码
期权的实时现金希腊值
Vega
Theta
Gamma
Delta
交易信息
持仓量
成交量
1档盘口信息
买隐波
买量
买价
卖价
卖量
卖隐波
净持仓
快速交易¶
点击管理界面的【快速交易】按钮,打开手动下单窗口:
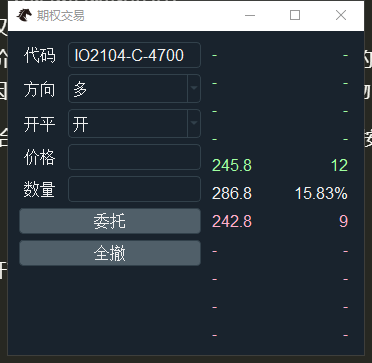
整体使用方法和VeighNa Trader主界面的交易组件相似,输入合约代码、买卖方向、开平方向、交易价格和数量后,点击【委托】按钮即可发出限价委托,点击【全撤】按钮即可一键全撤当前的全部活动委托。
双击T型报价中某一期权的单元格,可以快速填充本窗口的【代码】编辑框。
持仓希腊值¶
点击管理界面的【持仓希腊值】按钮,打开希腊值风险监控窗口:
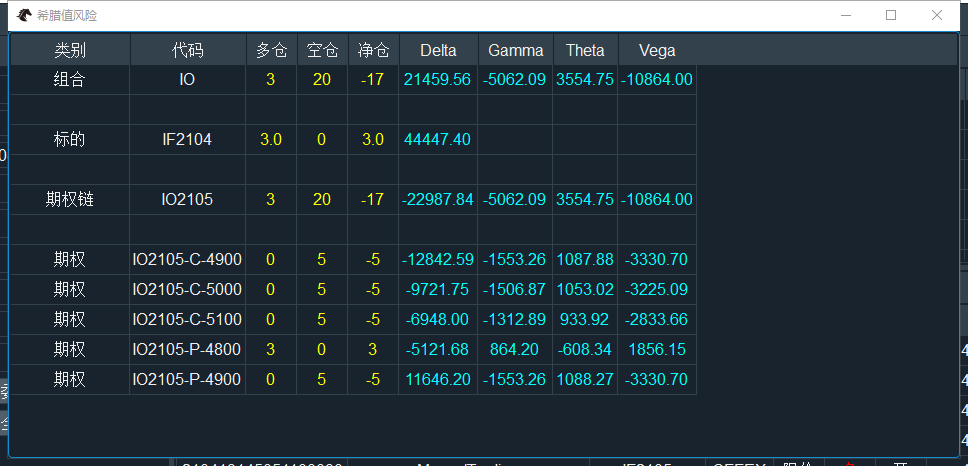
窗口中的监控信息分为四个维度:
交易组合(包括所有下属期权链和标的物汇总数据)
标的物合约
期权链(包括所有下属期权汇总数据)
期权合约
每个维度的监控信息包括:
持仓相关
多仓:当前的多头持仓
空仓:当前的空头持仓
净仓:多仓 - 空仓
总希腊值
Delta:标的价格涨跌1%对应的该维度盈亏金额
Gamma:标的价格涨跌1%对应的该维度的Delta变动
Theta:每过去一个交易日,该维度的盈亏金额
Vega:隐含波动率涨跌1%对应的该维度的盈亏金额
升贴水监控¶
点击管理界面的【升贴水监控】按钮,打开期权链定价升贴水校准幅度的监控窗口:
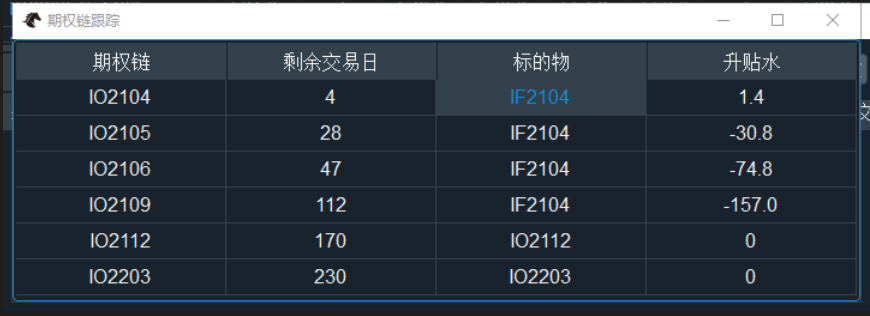
以上图为例,可以看到:
IO2104,以对应月份期货IF2104定价,升贴水接近0;
IO2105、IO2106、IO2109,以活跃合约IF2104定价,贴水依次增加;
IO2112、IO2203,以对应月份的合成期货定价,升贴水为0。
波动率曲线¶
点击管理界面的【波动率曲线】按钮,打开当前的市场波动率曲线监控图表:
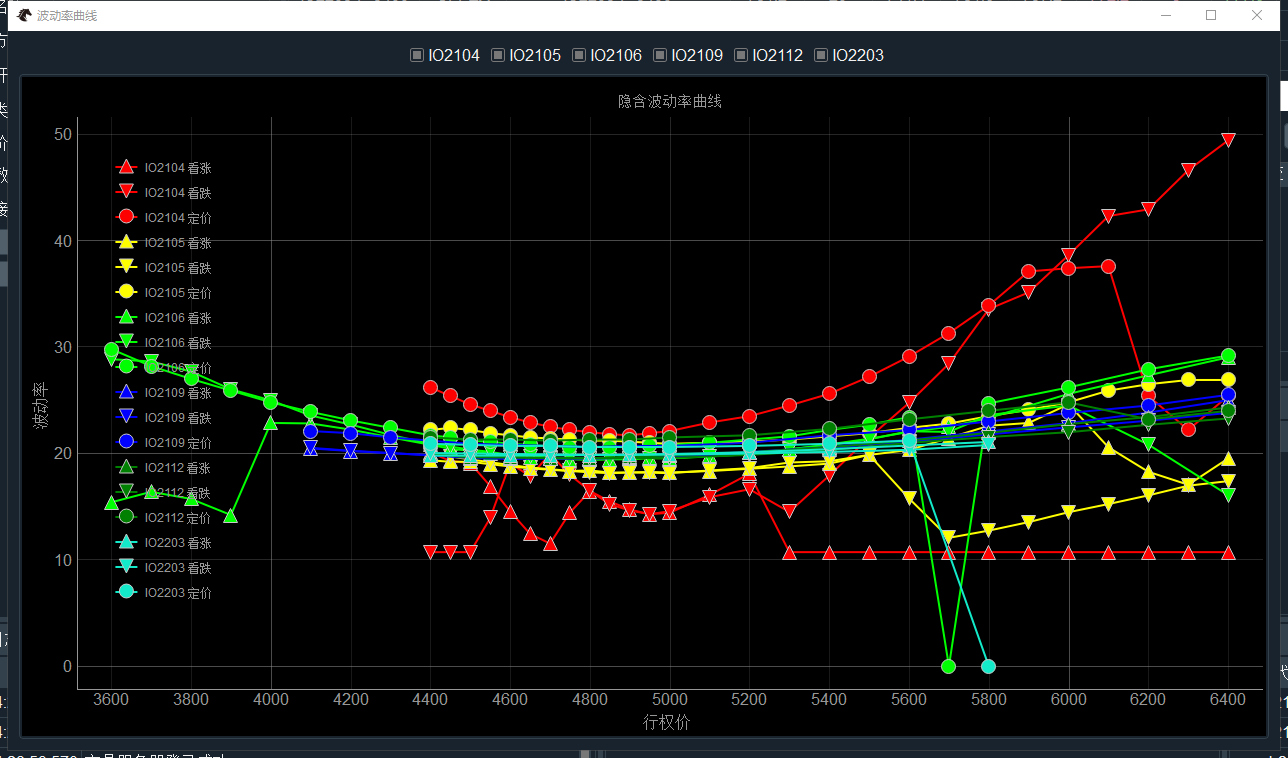
图表中每个期权链的波动率曲线采用不同颜色显示,具体颜色对应期权链的图例在左侧。
每个期权链会包括三条曲线:
向上箭头:该月份看涨期权的1档盘口隐含波动率中值,即买1价和卖1价盘口波动率的均值;
向下箭头:该月份看跌期权的1档盘口隐含波动率中值;
小圆点:该月份定价波动率的数值,定价波动率用于希腊值计算和电子眼交易,通过后面的【波动率管理】组件设置。
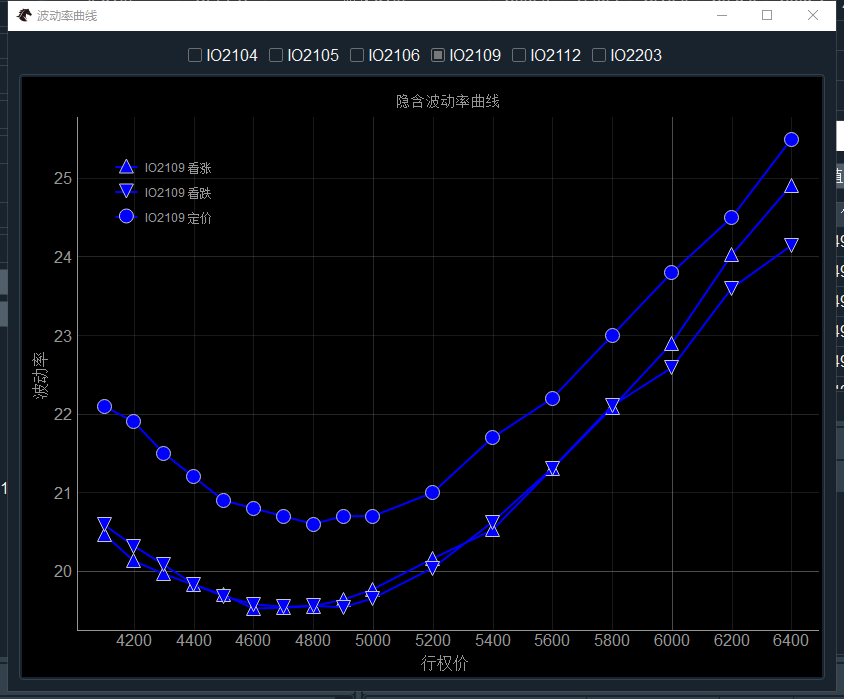
图表中显示的曲线通过窗口顶部每个期权链对应的勾选框来控制,可以根据需求进行调整,如下图中只显示了IO2109这一个期权链:
Delta对冲¶
点击管理界面的【Delta对冲】按钮,打开交易组合的Delta自动对冲功能:
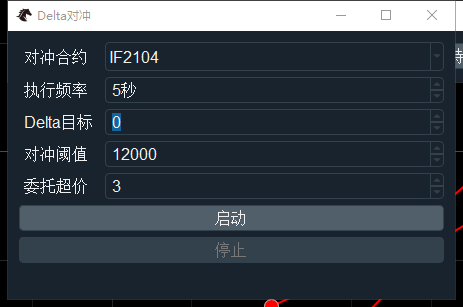
对冲标的:可以选择投资组合内的任意一个标的物合约;
执行频率:多久执行一次检查,判断是否要执行对冲;
Delta目标:如果触发对冲,将Delta值对冲到多少;
选择0,即为保持整体组合的Delta中性;
选择正数,即为保持整体组合的Delta多头敞口;
选择负数,即为保持整体组合的Delta空头敞口;
Delta范围:当仓位类型的Delta值偏离上述Delta目标超过多少时,触发对冲任务;
委托超价:发出对冲委托时,价格相对于对面盘口的超价;
点击【启动】按钮即可启动自动对冲功能,当读秒达到执行间隔时即会执行一次检查,如果满足条件则会启动TWAP算法执行对冲操作。
点击【停止】按钮即可停止自动对冲功能的运行。
情景分析¶
点击管理界面的【情景分析】按钮,打开交易组合整体持仓风险的压力测试和情景分析功能:
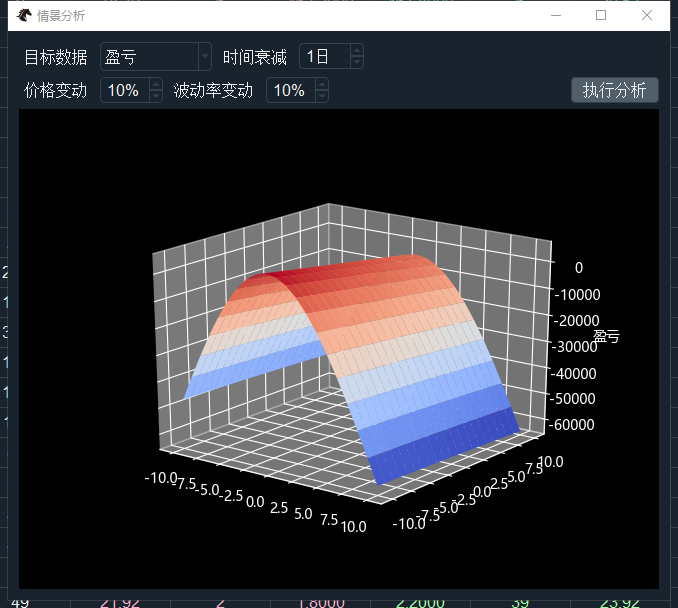
首先配置执行的分析任务:
目标数据:支持盈亏、Delta、Gamma、Theta、Vega;
时间衰减:交易日的衰减天数;
价格变动:
分析中价格的涨跌变动范围;
假设单前价格为100,变动为10%,则范围为90~110;
波动率变动:
分析中波动率的涨跌变动范围;
假设当前波动率为20%,变动为10%,则范围为10%~30%。
点击执行分析按钮后,压力测试引擎会根据当前的交易组合持仓,以及每个情景下的价格和隐含波动率情况,来计算对应的目标数据,并将结果绘制为3D曲面。
下图显示的是以Gamma值为计算目标,10%价格变动,15%波动率变动的结果:
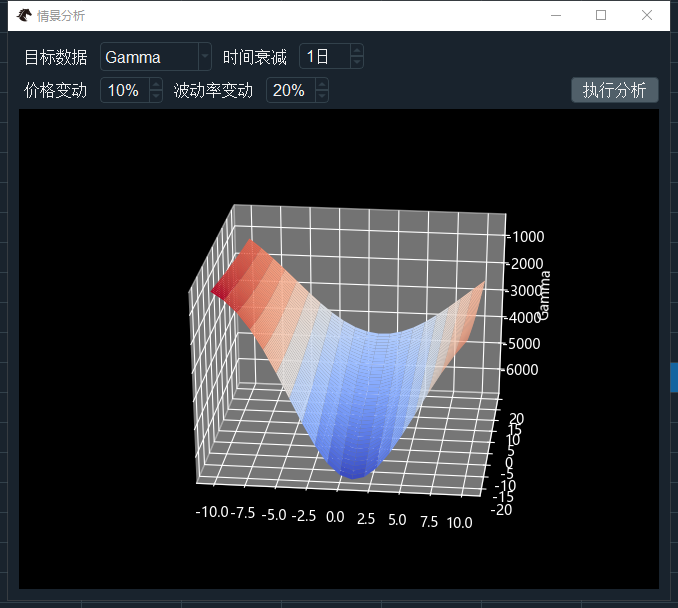
该3D图中的垂直轴为计算目标的数值,水平的两轴分别为价格和波动率的变动数值。
波动率管理¶
点击管理界面的【波动率管理】按钮,打开定价波动率管理界面:
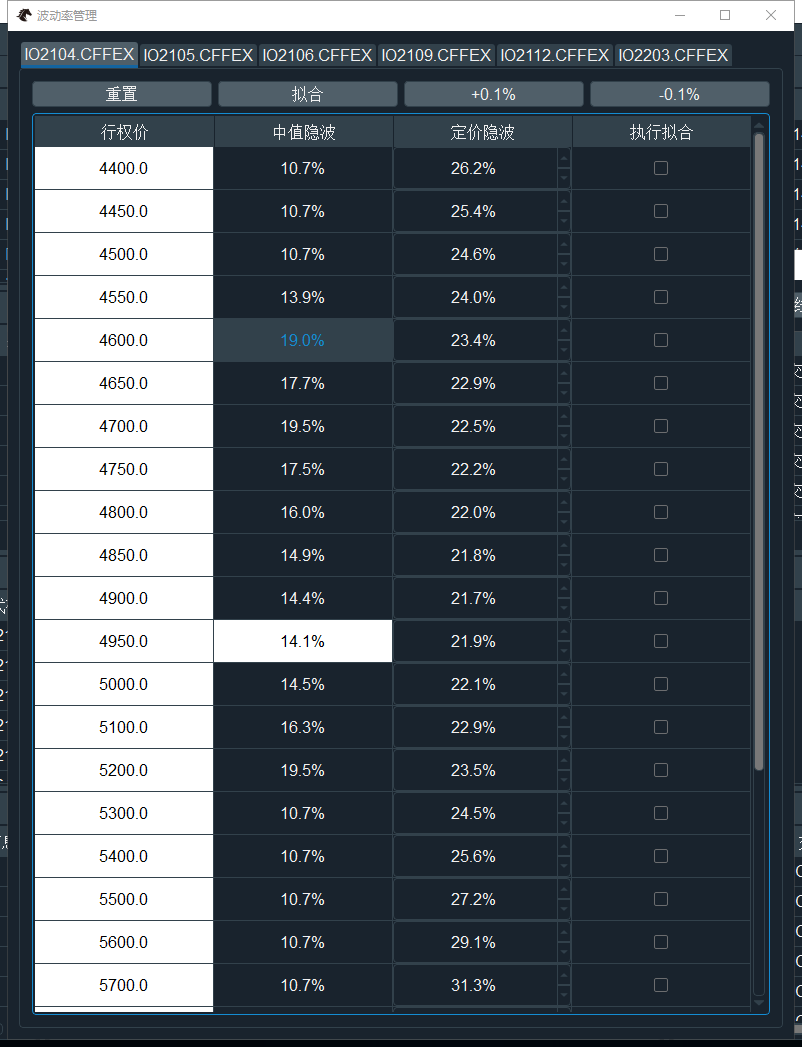
点击顶部的期权链标签切换对应期权链的定价波动率管理组件,第一次打开时下方表格中的【定价隐波】数值均为0。
首先进行定价曲线的初始化,点击顶部的【重置】按钮,将当前该行权价的虚值期权的中值隐波,映射到定价隐波上。
映射完成后可以在波动率图表中查看当前的定价波动率曲线形状,如果某一行权价的定价隐波和整体曲线相比存在不平滑的情况,则可以基于相对平滑的行权价的定价隐波对其进行拟合。
在组件表格中的【执行拟合】列,勾选要执行拟合的行权价勾选框,勾选完成后点击顶部的【拟合】按钮,即可基于OptionMaster内置的Cubic Spline(三项式差值)算法来执行波动率曲线的拟合。
拟合完成后如果还存在不满意的部分,则可以通过【定价隐波】列的滚动框来进行手动微调,点击上下箭头每次上升或者下跌0.1%,或者也可以直接输入想要修改的数值。
当因为对波动率曲线高低的整体观点,需要对曲线进行整体平移时,可以通过组件顶部的【+0.1%】和【-0.1%】按钮,来对所有行权价的定价波动率进行平移调整。
电子眼¶
点击管理界面的【电子眼】按钮,打开交易组合的电子眼自动套利算法功能:
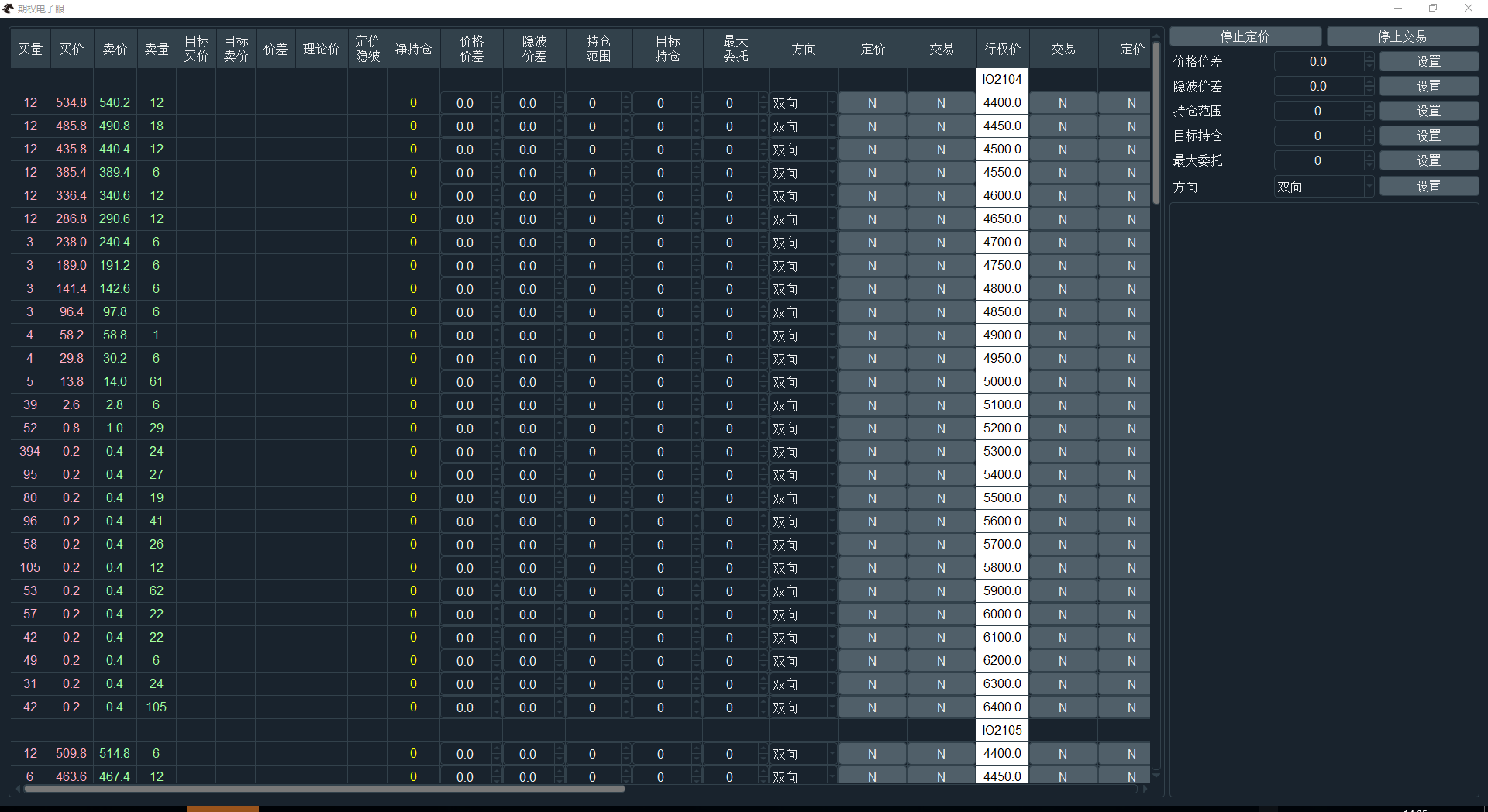
电子眼算法可以基于交易员预设的定价波动率曲线,在允许的持仓范围内自动捕捉市场上出现的瞬时交易执行机会,同时结合Delta自动对冲功能来保证投资组合的整体Delta中性。
电子眼界面类似T型报价分为左右区域,中间的白色为行权价,左侧为看涨期权,右侧为看跌期权。每个期权上对应存在一个独立的电子眼交易算法,交易员可以同时启动数百个交易算法(具体数量取决于CPU性能)而互不干扰。
每个电子眼算法的配置参数包括:
交易价差相关
价格价差
隐波价差
仓位限制相关
持仓范围
目标持仓
最大委托
单笔最大的委托数量
方向
算法允许的交易方向
包括只允许做多、只允许做空、允许双向交易
电子眼算法的执行流程如下:
基于定价波动率,计算期权的理论价
计算目标买卖的价差:
隐波价差的价格值 = 隐波价差 * 期权理论Vega值
交易价差 = max(价格价差, 隐波价差的价格值)
计算目标买卖价:
目标买价 = 理论价 - 交易价差 / 2
目标卖价 = 理论价 + 交易价差 / 2
以做多交易为例,当盘口卖1价格低于目标买价时,触发买入信号
计算本轮委托量:
算法持仓上限 = 目标持仓 + 持仓范围
剩余多头可交易量 = 算法多头持仓上限 - 当前净持仓
本轮委托量 = min(剩余多头可交易量,卖1量,最大委托量)
使用目标买价和本轮委托量,发出对应的交易委托
配置好算法参数后,点击该行的【定价】列的按钮启动算法的定价计算,如下图所示:
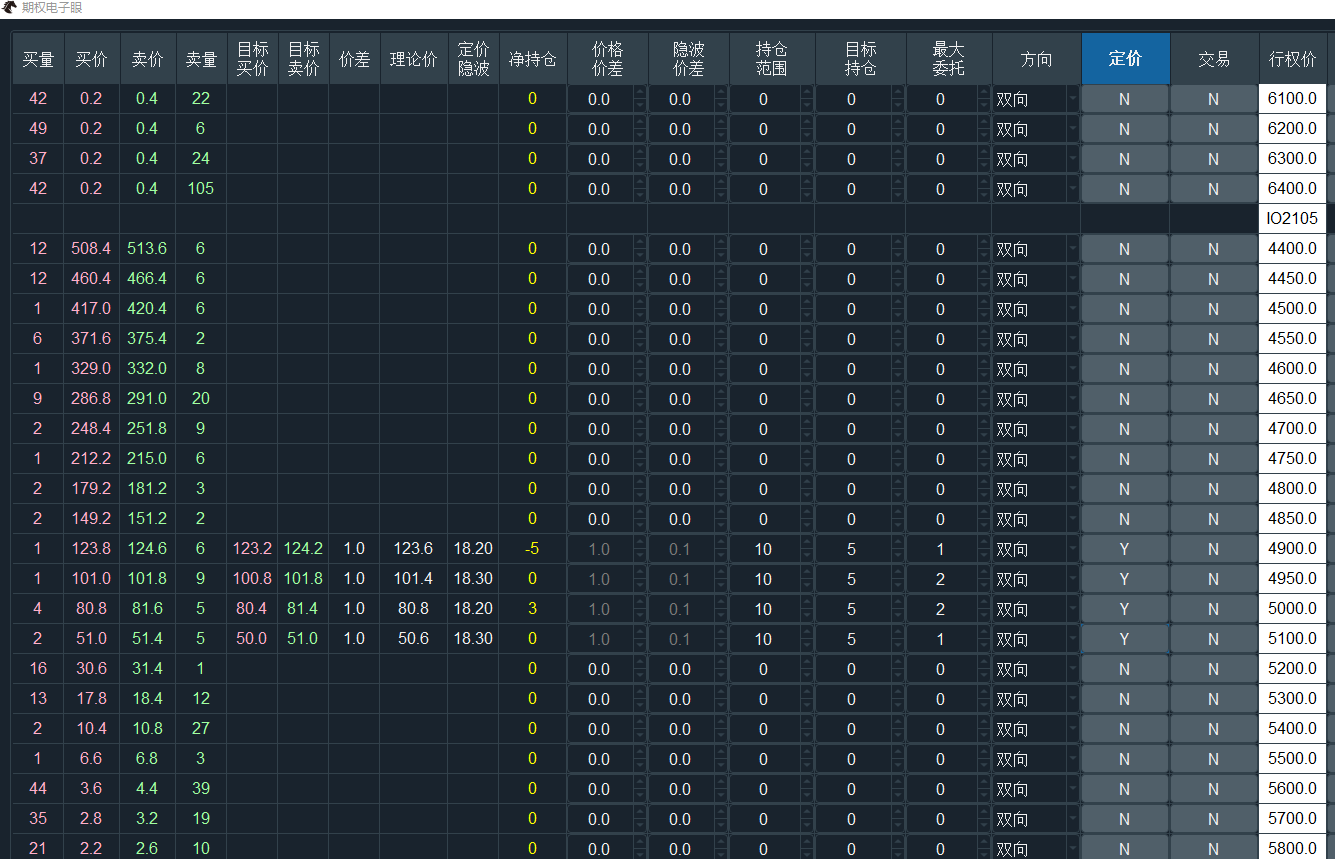
【定价】和【交易】按钮的状态显示:
为N时,代表算法当前未启动该任务
为Y时,代表算法已在执行对应的任务
启动定价的4个期权算法,会开始实时更新目标买卖价等相关数值。
此时点击【交易】列的按钮,即可启动算法的交易执行,当价格和持仓满足条件时就会自动发出交易委托,详细的算法运行状态日志信息可以通过右侧日志区域监控:
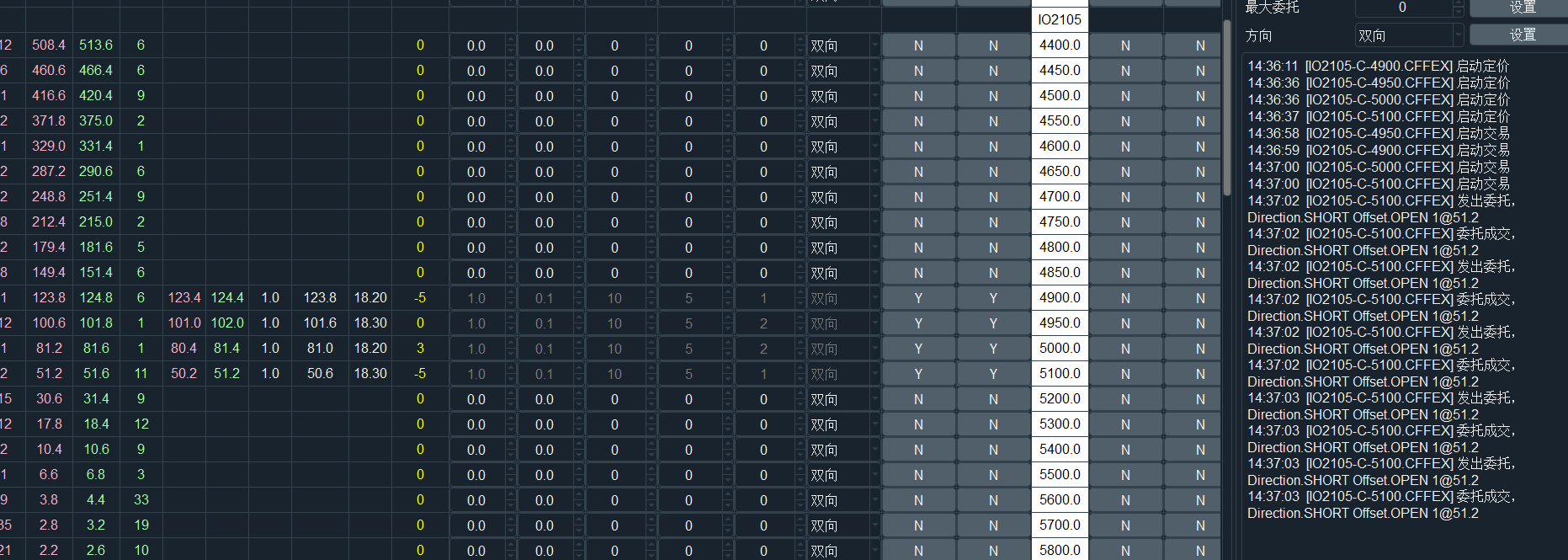
当需要对算法配置进行批量修改时,可以通过电子眼窗口的右上角的全局修改功能进行操作,更加方便快捷。





